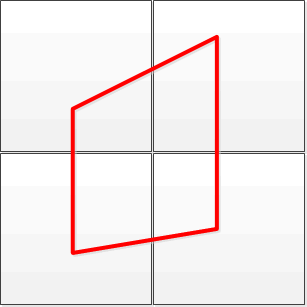
لنفترض أن لدينا شبكة (Grid) ثنائية البعد منتظمة بتباعد قدره h في كلا الإتجاهين (للسهولة)
ولنفرض أن لدينا شكلاً رباعياً (غير منتظم) محدداً بأربع نقاط ضمن هذه الشبكة.
السؤال هل هناك خوارزمية سريعة لحساب نسبة مساحة الرباعي في كل خلية في الشبكة من مساحة الرباعي الكلية؟
يعني النتيجة ستكون: الخلية رقم 2,3 تحوي 15% من مساحة الرباعي، بينما الخلية 2,4 تحوي 50% من مساحة الرباعي إلخ...

يمكن للتبسيط أيضاً افتراض أن الرباعي لا يقاطع أكثر من 4 خلايا نستطيع إيجادها بسهولة عن طريق إحداثيات زوايا الرباعي.

الطريقة البسيطة بحساب الرباعيات الجزئية المحتواة في كل خلية عن طريق
مقاطعة الحواف مع بعضها ثم حساب مساحة كل من هذه الرباعيات و تقسيمها على
مساحة الرباعي الكلية تبدو معقدة أكثر من اللازم كوني لا أحتاج إلى هذه
النقاط أو للمساحة بحد ذاتها. كما أن هذه الطريقة لا تستفيد من كون الشبكة
منتظمة.

أشعر أنه يجب أن يكون في هذه الحالة طريقة أفضل وأسرع، لكني لم أجدها بعد. هل لدى أحدكم خبرة بهذا الموضوع؟

هذا اقتراحي:
 
* قم بإيجاد المربع المحيط بخارج الشكل كإحداثيات في الشبكة (أعداد صحيحة، وليس عشرية).
* قم بإيجاد المربع المحيط بداخل الشكل كإحداثيات في الشبكة (أعداد صحيحة، وليس عشرية).
* كل الخلايا خارج المربع المحيط الخارجي فارغة بالتأكيد، وكل الخلايا في المربع المحيط الداخلي مليئة بالتأكيد.
* ادخل في حلقة لمعالجة كافة الخلايا المتبقية المحشورة بين المربعين المحيطين آنفي الذكر:
   - لكل خلية من هذه الخلايا، قم بتنفيذ عملية التقاطع الهندسية لمعرفة مساحة الخلية المغطاة من قبل الرباعي.
 
في ما سبق، نجد أنه لا مناص من تنفيذ حسابات التقاطع الهندسية، لكننا نحاول تحسين الأداء عن طريق استبعاد أكبر قدر ممكن من الخلايا من هذه الحسبة المكلفة.
 
يمكنك تطوير الفكرة السابقة وفقاً لطبيعة الرباعيات المتوقعة، فإن كانت أقرب للمربع المنتظم فإن الخوارزمية السابقة ناجعة، أما إن كانت رباعيات ذات زوايا حادة وغير موازية للمحاور الرئيسية، فمن الأفضل الاستعاضة عن المربع المحيط بطريقة أخرى لتقسيم الخلايا إلى الأصناف الثلاثة التي واجهناها: خارج 100%، داخل 100%، غير معروف.
 
مثلاً، تستطيع تحويل كل ضلع في الرباعي إلى خط قاطع يفصل بين فراغين: داخل الرباعي، وخارج الرباعي. بتكرار هذه العملية على كل الأضلاع تستطيع الوصول إلى ما سبق بمرونة أكثر، لكن على حساب المزيد من المعالجة في هذه الخطوة.
 
هناك المزيد من التحسينات الممكنة في حال ضمان بعض الشروط، لكنك لم تذكر أية معلومات إضافية، لذلك لا أستطيع افتراضها (مثلاً، هل من الممكن أن تقاطع خلية واحدة أكثر من ضلع دون أن تحوي رأساً من الرباعي؟).
 
بالتوفيق...

حسناً هاك خوارزمية أخرى 😄
 
هذه الخوارزمية "مسحية" تحتاج لبعض الذاكرة، لكنها سريعة جداً:
 
* احجز مصفوفة "ق" بعرض الشبكة حيث كل عنصر فيها يحمل رقمين: "أعلى" و "أسفل". هيّء كل عنصر في المصفوفة ليحمل القيمة الصحيحة القصوى في "أعلى" والقيمة الصحيحة السالبة القصوى في "أسفل".
 
* باستخدام خورزمية بريسنهام لتسميت الخطوط (line rasterization)، قم بتسميت خط بين كل رأس من رؤوس الرباعي.
   - لكل خلية من الخلايا التي تمر عليها في بريسنهام، قم بالآتي:
       1- تنفيذ عملية التقاطع الهندسية لمعرفة مساحة الخلية المغطاة من قبل الرباعي.
       2- خذ الإحداثي "س" للخلية، وقارن الإحداثي "ص" لها مع القيمتين "أعلى" وأسفل" في العنصر "س" من المصفوفة "ق".
           إن كان "ص" أصغر من "أعلى" فاجعل "أعلى" يحمل قيمة "ص"، وإن كان "ص" أكبر من "أسفل" فاجعل "أسفل" يحمل قيمة "ص".
 
بعد الانتهاء من تسميت الأضلاع الأربعة، تبقى لديك المصفوفة "ق". حيث كل عنصر "س" فيها الآن يحمل رقمين. الخلايا المحصورة بين [س،أعلى) و [س،أسفل) كلها مليئة 100% بالتأكيد.
 
هذه الخوارزمية أكثر مرونة من السابقة، لكنها تحتاج لمزيد من الذاكرة، كما أنك تحتاج لتفادي معالجة نفس الخلية أكثر من مرة أثناء التسميت (خاصة تلك التي تحوي الرؤوس)، وإلا فالنتيجة ستكون خاطئة (تستطيع استخدام مصفوفة بتات لتعليم الخلايا التي تمت معالجتها).

ممم... بالنسبة للخوارزمية الأولى فهي ما أقوم به الآن. الخوارزمية الثانية تحتاج إلى تسميت خط وهو أمر مكلف نسبياً مقارنة بإيجاد نقاط التقاطع بين الحواف.

أستطيع أن أفترض أن ضلعين من الرباعي متوازيان والرباعي لا يمكن أن يقاطع أكثر من 4 خلايا في وقت واحد كما قلت آنفاً.
أحاول أن أجد خوارزمية سريعة في هذه الحالة.
الحالة العامة بسيطة جداُ إذا استطعت أن أحل هذه الحالة الخاصة بزمن قصير نسبياً.

لم أفهم هذه النقطة... تقصد أن الرباعي دائماً بمساحة 4 خلايا؟

أعني أن أربع خلايا فقط في وقت واحد تستطيع أن تحوي على جزء من مساحة الرباعي

إذن الرباعي محصور في أربعة خلايا فقط؟ هكذا؟

نعم. لكن توزيع الزوايا الأربع قد يكون مختلفاً. فقد تكون زاويتان في خلية واحدة، أو ثلاث في خلية واحدة أو حتى أربع في خلية واحدة
لكن الرباعي يشترك بالمساحة مع أربع خلايا فقط من الشبكة...

ربما يجب أن أعطي معلومات أكثر عن المشكلة الكلية عل ذلك يساعد في إيجاد خوارزمية جيدة للمشكلة بأكملها
أنا أبدأ بشبكة منتظمة ثم أقوم بتغير إحداثيات نقاط الشبكة تبعاً لمعادلة معينة (معقدة نسبياً). الشبكة المعدلة غير منتطمة لكنها محتواة بالكامل في الشبكة المنتظمة الأساسية. الآن أريد أن أجد نسبة مساحات كل من الرباعيات في الشبكة المعدلة في خلايا الشبكة المنتظمة الأساسية.
كما تلاحظون لدي عدد كبير من الرباعيات. لذلك أحتاج إلى طريقة مثلى.

في هذه الحالة كلا من الخوارزميتين المقترحتين سابقاً غير مجديتين، فهما تحلان مسألة مختلفة.
 
نظرياً، لا يمكن لخوارزمية أن تحل هذه المسألة بتعقيد أقل من ثيتا(N)، حيث N هو عدد الرباعيات. الخوارزمية المباشرة لحل المسألة هي بالفعل تعمل في ثيتا(N). إذن، تحسين الأداء المطلوب ليس من الناحية الخوارزمية النظرية، وإنما من ناحية تطبيقية، مما يعني أنها مسألة برمجة وليس خوارزميات.
 
ما هو مجال العدد الكبير الذي نتحدث عنه هنا؟ آلاف؟ عشرات الألوف؟ ملايين؟

بالنسبة للعدد فهو في الآلاف. لكني يجب أن أقوم بهذا بمعدل ألفي مرة في كل خطوة زمنية. وفي حساباتي حوالي 10 آلاف خطوة زمنية
أتفق معك أنه قد يكون من غير المجدي تحسين أداء الخوارزمية (خاصة أني لا أطلب زمناً حقيقياً)

لذلك اسمح لي أن أغير من هدفي. أريد أبسط وأوضح طريقة لحل هذه المسألة. المشكلة أن البحث عن التقاطعات وتشكيل رباعيات جزئية فيه الكثير من الحالات (نقطة في كل خلية، نقطتين في خلية ونقطتين في خليتين، ثلاث نقطة في خلية، نقطتين في كل خلية، أربع نقط في خلية) أضرب ذلك بالاحتمالات العدة التي تنتج عن تدوير الرباعي. لم أكتب الكود العام بعد لكن يبدو أنه سيكون بشعاً جداً.
إذاً هل لديك طريقة لتبسيط هذه الخوارزمية؟ وربما بناء معطيات يجعل هذا الأمر سهلاً نسبياً؟

ملاحظة: يبدو حل التسميت من السهولة بمكان لكني لا أفضله في هذه الحالة لأسباب عدة