

 همام البهنسي
مشاركة 1
في 07 يونيو 2017 04:27 ص
همام البهنسي
مشاركة 1
في 07 يونيو 2017 04:27 ص
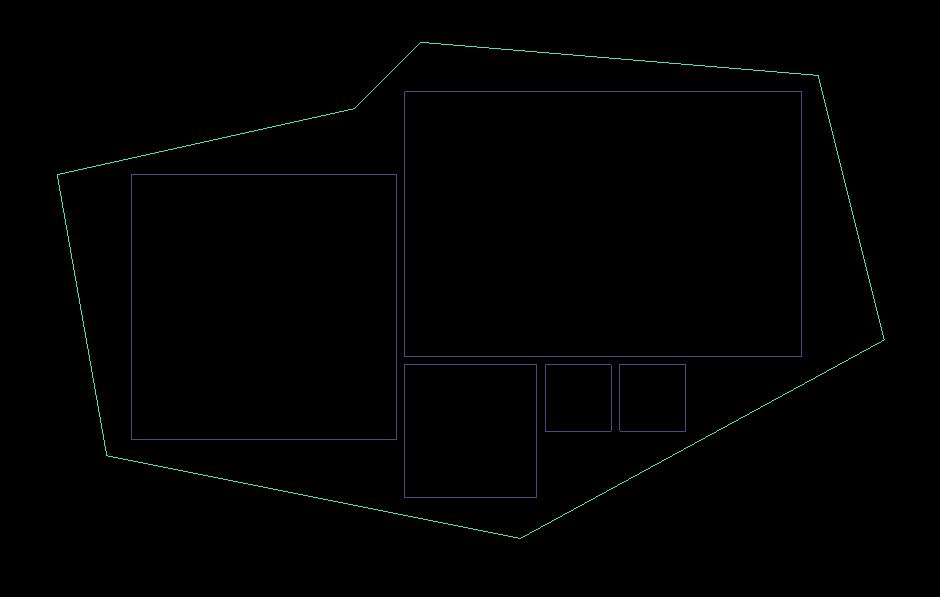
أحاول البحث عن خوازمية سريعة لحل المسألة التالية:
الناتج المتوقع من الخوارزمية
شكراً مسبقاً على أي أفكار أو اقتراحات!
- لدينا مضلع غير منتظم و مغلق.
- لدينا مصفوفة من المستطيلات ذات الأحجام المختلفة.
الناتج المتوقع من الخوارزمية
- رقم التسلسل للمستطيل الذي تم اختياره من المصفوفة.
- مصفوفة التحويل لكل مستطيل بالنسبة للمضلع.

شكراً مسبقاً على أي أفكار أو اقتراحات!


 وسام البهنسي
مشاركة 2
في 07 يونيو 2017 07:48 ص
وسام البهنسي
مشاركة 2
في 07 يونيو 2017 07:48 ص
ربما كبداية نستطيع القول أنه لا حاجة لدعم التدوير بشكل صريح. نستطيع جعل الخوارزمية تتعامل فقط مع مجموعة مستطيلات معطاة في مصفوفة. ولدعم التدوير، نضيف كل مستطيل مرتين إلى المصفوفة. مرة بشكل طولي والثانية بشكل عرضي عن طريق تبديل الأبعاد فقط.
مثلاً:
3×4 يضاف أيضاً ك 4×3
أما عن البقية، تذكرني هذه الخوارزمية بمسألة اللص أو Knapsack الشهيرة، لكن الأخيرة ليست ثنائية البعد... همم...
مثلاً:
3×4 يضاف أيضاً ك 4×3
أما عن البقية، تذكرني هذه الخوارزمية بمسألة اللص أو Knapsack الشهيرة، لكن الأخيرة ليست ثنائية البعد... همم...
وسام البهنسي
مبرمج في إنفيديا وإنفريمز
مبرمج في إنفيديا وإنفريمز


 وسام البهنسي
مشاركة 3
في 07 يونيو 2017 07:54 ص
وسام البهنسي
مشاركة 3
في 07 يونيو 2017 07:54 ص
وهذا رابط لمسألة نابساك على ويكيبيديا:
https:/
وكما تقرأ، لا يوجد حل سريع بزمن خطي لهذه المسألة. وتعتبر البرمجة الديناميكية من الطرق المتبعة لحل المسألة. لذلك يمكننا القول بأمان أن مسألة ملء المضلع ستكون أبطأ وأبطأ.
https:/
وكما تقرأ، لا يوجد حل سريع بزمن خطي لهذه المسألة. وتعتبر البرمجة الديناميكية من الطرق المتبعة لحل المسألة. لذلك يمكننا القول بأمان أن مسألة ملء المضلع ستكون أبطأ وأبطأ.
وسام البهنسي
مبرمج في إنفيديا وإنفريمز
مبرمج في إنفيديا وإنفريمز

 Ibrahim H Alnoor
مشاركة 4
في 07 يونيو 2017 09:07 ص
Ibrahim H Alnoor
مشاركة 4
في 07 يونيو 2017 09:07 ص
تحية طيبة,
استخدم for - each بدءا من الاكبر الى الاصغر, وداخل كل حلقة استخدم do - while, وأما الـCondition يكون ان تستخدم نفس المستطيل لعدد خير محدود الى أن تصل للحد الذي لا يمكن استخدامه اكثر من ذلك, ثم انتقل الى المستطيل التالي في For - Each
وطبعا راح تستخدم التدوير ودوال الـ Collision detection في كل مرة لكل مستطيل
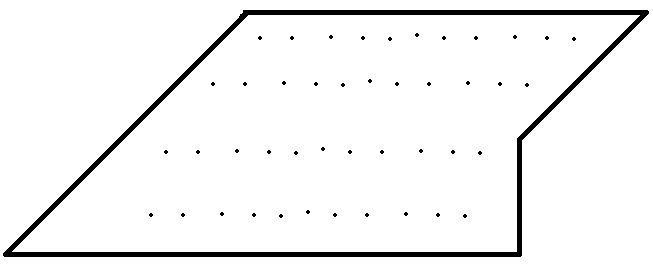
قبل كل ذلك, حاول بطريقة او بأخرى ان تملأ المضلع الغير منتظم بعدد من النقاط Vertices تكون كمواضع وأماكن تضع فيها المستطيلات ,وتختبر امكانية وضع كل مستطيل عليها.
نظريا طبعا
بمعنى:
For each Rect
Do
For each Vertex
\\ Your stuff :)
Next
While Can fit
Next
عارف انه احتمال حلي نظريا سهل نظريا لكن تطبيقه صعب, مجرد محاولة اتمنى تتقبلها.
تحياتي
استخدم for - each بدءا من الاكبر الى الاصغر, وداخل كل حلقة استخدم do - while, وأما الـCondition يكون ان تستخدم نفس المستطيل لعدد خير محدود الى أن تصل للحد الذي لا يمكن استخدامه اكثر من ذلك, ثم انتقل الى المستطيل التالي في For - Each
وطبعا راح تستخدم التدوير ودوال الـ Collision detection في كل مرة لكل مستطيل
قبل كل ذلك, حاول بطريقة او بأخرى ان تملأ المضلع الغير منتظم بعدد من النقاط Vertices تكون كمواضع وأماكن تضع فيها المستطيلات ,وتختبر امكانية وضع كل مستطيل عليها.

نظريا طبعا
بمعنى:
For each Rect
Do
For each Vertex
\\ Your stuff :)
Next
While Can fit
Next
عارف انه احتمال حلي نظريا سهل نظريا لكن تطبيقه صعب, مجرد محاولة اتمنى تتقبلها.
تحياتي

 اونلاين
مشاركة 5
في 07 يونيو 2017 05:15 م
اونلاين
مشاركة 5
في 07 يونيو 2017 05:15 م
أول فكرة برضو كانت ال knapsack.
تاني فكرة جت في بالي الtesselation عموما وطبعا غير مناسبة ابدا عشان مش مسموح بأي فواصل.
بعد شوية بحث وتفكير عرفت انها تعتبر packing problem، ومن غير ما افتي في ال hardness بتاعتها لوقابلتني المشكلة دي غالبا هبسطها للتالي:
loop while pixel not tested
(find the largest possible rectangle (not from the list of rectanlges but any rectangle at all
mark the rectangle area as tested
end loop
وداخل جوة "اكبر مستطيل" نلاقيه، وهنا متفقين انه اكبر مستطيل ممكن مش اكبر مستطيل من الليستة بتاعتنا ولا حاجة. المهم جواه نخش ننفذ كود يجيبلنا packing of rectangles from our list into an arbitary rectangle وممكن مثلا بgreedy approach بعد ما يتم ترتيب ليستة المستطيلات بتاعتنا.
الحل ده يمكن مش اسرع حل، الحل ده الأكيد انه مش optimal، بل حتى مش unique، اتأكدت بنفسي ان حل مسألة "اكبر مستطيل ممكن جوة مضلع" مش unique، لكن لو اتطلب مني فده اقتراحي لتبسيط المشكلة، وتبسيط المشكلة مش دايما عيب.
-هبه
تاني فكرة جت في بالي الtesselation عموما وطبعا غير مناسبة ابدا عشان مش مسموح بأي فواصل.
بعد شوية بحث وتفكير عرفت انها تعتبر packing problem، ومن غير ما افتي في ال hardness بتاعتها لوقابلتني المشكلة دي غالبا هبسطها للتالي:
loop while pixel not tested
(find the largest possible rectangle (not from the list of rectanlges but any rectangle at all
mark the rectangle area as tested
end loop
وداخل جوة "اكبر مستطيل" نلاقيه، وهنا متفقين انه اكبر مستطيل ممكن مش اكبر مستطيل من الليستة بتاعتنا ولا حاجة. المهم جواه نخش ننفذ كود يجيبلنا packing of rectangles from our list into an arbitary rectangle وممكن مثلا بgreedy approach بعد ما يتم ترتيب ليستة المستطيلات بتاعتنا.
الحل ده يمكن مش اسرع حل، الحل ده الأكيد انه مش optimal، بل حتى مش unique، اتأكدت بنفسي ان حل مسألة "اكبر مستطيل ممكن جوة مضلع" مش unique، لكن لو اتطلب مني فده اقتراحي لتبسيط المشكلة، وتبسيط المشكلة مش دايما عيب.
-هبه

 ياسر جفال
مشاركة 6
في 08 يونيو 2017 05:55 ص
ياسر جفال
مشاركة 6
في 08 يونيو 2017 05:55 ص
ربما الخطوة الأولى هي الحصول على أكبر مستطيل ممكن داخل المضلع، ومن ثم من خلال الاستدعاء الذاتي recursion نبحث عن أكبر مستطيل داخل المضلعات الناتجة عن قطع المستطيل الأكبر. شرط التوقف هو أن تصبح جميع المضلعات الناتجة يمكن أن يحتويها أصغر مستطيل لدينا.
بهذا نكون قد تخلصنا من مسألة المضلع ويبقى أن نمر على المستطيلات الناتجة واحدا تلو الآخر ونملأها بالمستطيلات حسب الشروط. هذا بشكل عام، الشيطان في التفاصيل والله أعلم
بهذا نكون قد تخلصنا من مسألة المضلع ويبقى أن نمر على المستطيلات الناتجة واحدا تلو الآخر ونملأها بالمستطيلات حسب الشروط. هذا بشكل عام، الشيطان في التفاصيل والله أعلم


 همام البهنسي
مشاركة 7
في 09 يونيو 2017 03:30 ص
همام البهنسي
مشاركة 7
في 09 يونيو 2017 03:30 ص
شكرا للجميع على الاقتراحات، المسألة كما ذكر مشتقة من مسألة الحقيبة ولكن مع طبقة تعقيد جيومترية للتعامل مع المضلع. تطبيق الحل الكلاسيكي لمسألة الحقيبة من خلال البرمجة الديناميكية وكشف التقاطع بين المستطيلات والمضلع بطيء جدا.
اقتراح الأخ إبراهيم لتفادي كشف التقاطعات من خلال التعامل مع شبكة من النقط المسبقة اقتراح جذاب وبلا شك أسرع من الحل القسري bruteforce.
أيضا اقتراح الأخت هبه و الأخ ياسر يبدو جيد لتبسيط المسألة وإيجاد حل مقبول.
قبل البدء بتنفيذ أي من هذه الحلول، سأبذل المزيد من الوقت للتفكير بشروط المسألة لعلي أتمكن من تبسيطها أكثر.
شكرا للجميع مرة ثانية 😊
اقتراح الأخ إبراهيم لتفادي كشف التقاطعات من خلال التعامل مع شبكة من النقط المسبقة اقتراح جذاب وبلا شك أسرع من الحل القسري bruteforce.
أيضا اقتراح الأخت هبه و الأخ ياسر يبدو جيد لتبسيط المسألة وإيجاد حل مقبول.
قبل البدء بتنفيذ أي من هذه الحلول، سأبذل المزيد من الوقت للتفكير بشروط المسألة لعلي أتمكن من تبسيطها أكثر.
شكرا للجميع مرة ثانية 😊