أعلم أن منحنيات Bezier هي حالة خاصة من منحنيات NURBS, لكن ما هي معادلات تحويل منحنيات Bezier إلى NURBS? اليحث على الـ google لم يعطني أي نتائج مفيدة

أيضاً هل لدى أحدكم أي مرجع يشرح الـ Knots لمنحنيات NURBS بشكل مفصل؟

شكراً

لا يوجد "معادلة" للتحويل لأن معادلة Bezier هي أساساً حالة خاصة من معادلة الـ NURBS، لذا كل ما عليك فعله هو استخدام معادلة الـ NURBS بدلاً من Bezier. النقطة المهمة هنا أن منحني الـ NURBS يحتاج إلى مجموعة معلومات إضافية مهملة في Bezier وهي مصفوفة العقد (knots). يمكنك توليد هذه المصفوفة ببساطة للحصول على منحني NURBS مطابق لمنحني Bezier. سأشرح الطريقة بمثال منحني Bezier القياسي (تكعيبي):
لدينا المنحني معرف بنقاطه الأربع:

P1 = (0,0)  // Start point
P2 = (0,100)  // Start point tangent
P3 = (100,-100)  // End point tangent
P4 = (100,0)  // End point

منحني الـ NURBS المقابل هو:

Control Points = { P1, P2, P3, P4 }
Knots = { 0,0,0,0, 1,1,1,1 }

المثال السابق فقط لقطعة Bezier واحدة من الدرجة الثالثة. للتعميم، فإن القاعدة هي:
- مصفوفة نقاط التحكم تنقل كما هي للـ NURBS (لمعامل الوزن يتم استخدام 1 دائماً).
- مصفوفة العقد تتكون من العدد التالي من العناصر:
درجة المنحني + عدد نقاط التحكم + 1
يتم تعبئتها كالآتي:
* مجموعة العناصر الأولى المكونة من "درجة المنحني+1" عنصر يتم جعلها تساوي 0.
* مجموعة العناصر الأخيرة المكونة من نفس العدد السابق يتم جعلها تساوي 1 (أو أية قيمة غير الصفر، كـ 24 مثلاً).
* العناصر المتبقية في المنتصف يتم تعبئتها بطريقة الاستقراء الخطي بين 0 و 1 (أو العدد الذي اخترته لمجموعة العناصر الأخيرة، كـ 24 مثلاً)، بحيث يكون تكرار العقدة (multiplicity) يساوي درجة المنحني.

لمنحني Bezier من الدرجة السابعة من قطعة واحدة يتم تحويله لمنحني NURBS بمصفوفة العقد التالية:
0,0,0,0, 0,0,0,0, 1,1,1,1, 1,1,1,1

لمنحني Bezier من الدرجة الثالثة من قطعتين، يتم تحويله بمصفوفة العقد:
0,0,0,0, 1,1,1, 2,2,2,2

مصفوفة العقد لمنحني Bezier من الدرجة الثانية من 3 قطع:
0,0,0, 1,1, 2,2, 3,3,3


وهكذا...

(هذه الطريقة تم تجريبها مع خوارزمية De Boor لحل الـ NURBS وتعطي تطابق تام)


المرجع الأمثل هو كتاب الـ NURBS (أو The NURBS book كما يدعى) من تأليف Piegl وTiller. يمكنك أيضاً قراءة مقدمة لا بأس بها في موقع برنامج Rhinoceros3D حيث أنه مختص بهذا النوع من الـ modelling:
http://www.rhino3d.com/nurbs.htm

باختصار هي عقد تحدد شد المنحني لنقطة التحكم الموافقة. في الحقيقة هي نسبة تأثير العقد المجاورة على النقطة الحالية.. لكن الشرح الأول أبسط للفهم أحياناً...

(لقد قمت بتعديل هذه المقالة مرتين وذلك بسبب الأخطاء التي ارتكبتها في أول محاولتين. آسف، لكنني كنت بعيداً عن الموضوع لفترة جيدة)

شكراً وسام على هذا الشرح المستفيض (شكر متأخر... أعلم ذلك، لكن أن تأتي متأخراً خير من ألا تأتي أبداً☺

لكن يبدو أن هناك مشكلة ما في هذه الخوارزمية في حال المنحنيات المؤلفة من أكثر من قطعة.

كنت أحاول أن أرسم قطعاً ناقصاً (في الحقيقة كنت أنوي أن تكون دائرة☺ فبدأت بأن أرسم 8 منحنيات Bezier من الدرجة الثانية وبنقاط تحكم مشتركة (بالقيم فقط.. لكنها مكررة في الحقيقة). ثم قمت بـ"تحويل" هذه المنحنيات إلى منحنيات NURBS باستخدام مصفوفة الـ Knots
0,0,0,1,1,1
لكل منحن وقد ظهرت الشكل كالتالي (على XSI):


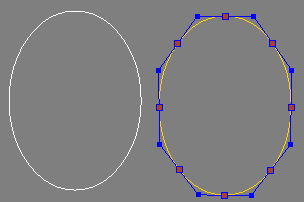
ثم قررت أن أدمج هذه المنحنيات كلها في منحن NURBS واحد حتى لا يكون هناك تكرار في النقط. فاستخدمت نفس نقاط التحكم مع منحنيات من الدرجة الثانية ومصفوفة الـ Knots التالية:
0,0,0,1,2,3,4,5,6,7,8,9,10,11,12,14,15,15,15
لكن النتيجة كانت مختلفة تماماً:


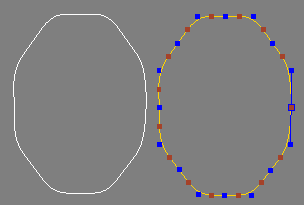
يبدو أنني نسيت أو لم أفهم شيئاً معيناً.

كسؤال جانبي: هل بأمكاني دمج منحنيات Bezier من الدرجة الثانية والثالثة في منحن NURBS واحد؟ بدون إضافة نقاط إضافية...

شكراً جزيلاً

المثير للاهتمام هو أنني أرى تطابق تام بين المنحنيين في الصورة إياها... أين المشكلة بالضبط؟


كلا. لأن هذا يعني وجود عدم استمرارية بين القطع. إذا أجبرت منحنياتك لتدمج قطع من مختلف الدرجات فإنك ستجدها تتصل مع بعضها بمنحنيات صغيرة عند نقاط الالتقاء.
يجب التعامل مع هذه المنحنيات كمنحنيات مستقلة، أو بإضافة عقد إضافية تضمن الانقطاع المرغوب. سيكون من المثير للاهتمام معرفة كيف يكون رد فعل نقطة يتم استقراؤها على هذا المنحني خلال الزمن (أتوقع قفزات مختلفة بالسرعة).

هل من الممكن أن تكتب إحداثيات نقاط التحكم الثمانية للمنحني المرسوم في الصورة؟ سأقوم بتجريب الأمور هنا لفترة...

ها هم...
0.876363636363636, -1.875
0.876363636363636, -2.0095
0.807090909090909, -2.10475
0.737818181818182, -2.2
0.64, -2.2
0.542181818181818, -2.2
0.472909090909091, -2.10475
0.403636363636364, -2.0095
0.403636363636364, -1.875
0.403636363636364, -1.7405
0.472909090909091, -1.64525
0.542181818181818, -1.55
0.64, -1.55
0.737818181818182, -1.55
0.807090909090909, -1.64525
0.876363636363636, -1.7405
0.876363636363636, -1.875

حسناً، لقد ارتكبت غلطة أخرى في طريقة تعبئة مصفوفة العقد (تباً لهذه المراجع الغامضة). المهم، لقد قمت بتعديل ردي الأصلي وهو الآن يحتوي على الحسابات الصحيحة (لم أنتبه لموضوع التكرار هذا رغم أنه مذكور في نفس المرجع الذي ذكرته في تلك المشاركة).

لقد قمت بتجريب الحسابات الجديدة على المنحني الذي أعطيتني إياه وهو يظهر بشكل صحيح الآن...

تعقيباً على سؤالك الثاني عن إضافة منحنيات من درجات مختلفة مع بعضها فإنني أريد أن أذكر أيضاً أنه إضافة للانقطاع فإن خوارزميات حساب الـ NURBS الاعتيادية لا يمكنها التعامل مع هذا النوع من المعلومات أساساً. فهي تفترض أن جميع القطع تتشارك بنفس الدرجة. يمكنك رسم القطع مختلفة الدرجات بشكل مستقل طبعاً. إلا أن الحل الأمثل هو ترقية درجة كل القطع حتى تصبح متساوية فيما بينها، قبل دمجها في سلسلة واحدة. عملية الترقية تتضمن طبعاً إضافة نقاط تحكم جديدة للحفاظ على الشكل الأصلي، لكن سؤالك صريح بأنك لا ترغب في إضافة نقط جديدة...

يبدو أن الخوارزمية لا زالت تحوي بعض المشاكل.
لقد جربت التالي:
1. إنشاء Cubic Bezier بنقاط التحكم: [0,2], [1,1], [1,1], [0,0]
و مصفوفة العقد: 0,0,0,0,1,1,1,1 كما تحدد الخوارزمية
2. إنشاء Quadratic Bezier بنقاط التحكم: [0,2], [1,1], [0,0]
و مصفوفة العقد: 0,0,0,1,1,1 كما تحدد الخوارزمية

متوقعاً ان أحصل على منحنيين متطابقين، لكني تفاجئت أن المنحني الأول يختلف بشكل كبير عند المنتصف عن المنحني الثاني (الذي أعتقده هو المنحني الصحيح)
هل نسيتُ شيئاً ما؟
شكراً

تباً من قال أنه هكذا يتم تحويل الـ Quadratic bezier إلى Cubic Bezier? آسف حقاً. الخوارزمية تعمل بشكل جيد جداً في كل درجات Bezier.

:)