السلام عليكم

الكل يعرف اهمية موضوع ايجاد اقصر طريق بطريقة مناسبة في معظم او كل الالعاب الحالية وكثير من برامج المحاكاة
ولان الموضوع يعتمد بشكل كبير حسب حالة المشهد المراد ايجاد اقصر مسار فيه وكذلك علي عدد الوحدات ونوع هيكل البيانات التي يتم وصف البيئة فيه

قرأت انه هناك طريق كثير جدا لحساب اقل تكلفة لايجاد المسار وهناك الاتي:-
1- لايجاد المسار بين نقطتين يمكننا استخدام خوارزميات عديدة اكثرها انتشارا ومرونة هو ال *A
يمكنك ان تجد كثير جدا من موارد الانترنت التي تشرح وتوضح الكثير من الامثلة وتطبيقها بلغات مختلفة
2- لايجاد المسار بين نقطة واحدة كبداية وعدة نقاط كنهاية يمكن استخدام خوارزم Dijkstra's
وهو ايضا لديه الكثير من الشرح والموارد علي النت والامثلة

لكن  هناك خوارزم سمعت عنه وهو Floyd وبالبحث عنه وجدت انه يقوم بايجاد اقصر طريق بين كل نقطتين موجودتين في Graph او Grid
لقد ارفقت ملف عرض باور بوينت وجدته يصف كيفية حساب ال solution matrix بطريقة ال Floyd
وهناك الرابط الاتي وهو جيدا ايضا
http://compprog.wordpress.com/2007/11/15/all-sources-shortest-path-the-floyd-warshall-algorithm/

المشكلة التي تواجهني هي انني لم افهم كيفية استخراج المسار الذي يمثل اقصر طريق من المصفوفة الناتجة والتي يتم تخزين فيها قيم اقصر طريق بين كل نقطتين
- لقد ارفقت مثال ايضا لكنه فقط يقوم بتطبيق الـ Graph الموجودة في الرابط السابق لكنه يقوم بحساب المصفوفة ولا يقوم باستخراج المسار
طريقة استخراج المسار  مذكورة في ملف الباور بوينت لكني لم افهمها

اتمني ان يساعد احد بوضع طريقة يوضح فيها كيفية الاستفادة من مصفوفة floyd لمعرفة المسار الاقل والاقصر في التكلفة

ملاحظة يمكننا جعل هذا المقال بداية لمناقشة خوارزميات ايجاد الطرق
في انتظار التعليقات والاراء 😄
وجزاكم الله خيرا

وعليكم السلام...
 
بداية أشكرك أخي أحمد على هذا الموضوع الشيق وعلى طرحك لهذا الخوارزمية، لأني بصراحة لم اسمع بها من قبل رغم تعمقي مؤخراً في خوارزميات تخطيط الحركة (Motion Planning) ضمن دراستي الحالية.
لذلك سأحاول المساهمة ضمن معلوماتي في هذا الموضوع قدر الامكان...




بالنسبة للـ A* اوفقك الرأي بانها واسعة الانتشار والتطبيق وخصوصاً في مجال الألعاب ولكنها للأسف تعاني من قائمة طويلة جداً من المحدوديات، لذلك لايمكننا وصفها بأنها الأكثر مرونة...طبعاً لنقاش هذه المحدوديات نحن بحاجة لمشاركات منفصلة وطويلة، ولكن على سبيل المثال:
أحد هذه المحدوديات هو عدم فعاليتها في ايجاد الطريق أو المسار ضمن بيئة متعددة الأبعاد (أي أكثر من ثلاثة أبعاد أو بشكل عام فراغ من البعد N). عادة في مشاريع الألعاب لا نواجه مثل هذا النوع من المسائل، معظم الألعاب يتم التعامل معها كمسألة بفراغ ثنائي البعد، ولكن في الكثير من التطبيقات الأخرى وخصوصاً تطبيقات الروبوتات من الشائع جداً أن يكون المسار المطلوب ايجاده ضمن فراغ سباعي البعد أو أكثر.
قد لا تكون الفكرة واضحة من الناحية العملية ولكني لا أريد التعمق هنا في هذا الموضوع لكي لا نخرج كثيرا عن الموضوع الأساسي ولكن إن احببت يمكننا النقاش في مشاركة منفصلة.
 
 

 
للدقة، ما تقوم به هذه الخوارزمية هو إيجاد المسار الأقل تكلفة وليس الأقصر، حيث يمكنك الاستفادة منها لتعريف أي عدد من الخصائص والقيام بإيجاد المسار الأمثلي بناءً على هذه الخصائص أو الأوزان. بالطبع اول ما يتبادر للذهن هو تعريف أطوال أو مسافات للحصول على اقصر مسافة... ولكن ما يهمنا من هذا التعميم هو اظهار التشابه بين طريقة عمل هذه الخوارزمية وبين طرائق الاستمثال (Optimization Problems) المعروفة في بحوث العمليات (Operation Research)، حيث هناك الكثير من الطرق المستخدمة في إيجاد المسار الأقصر في بحوث العمليات مثل البرمجة الديناميكية (Dynamic Programming). المثال التالي يظهر طريقة حل مسألة إيجاد مسار باستخدام أسلوب البرمجة الديناميكية:
 
مثال...
يبين الشكل التالي المخطط الشبكي المعبر عن المدن المنتشرة بين المحافظتين D و H حيث تعطى تكلفة النقل بين المدن المختلفة على طول الخطوط الواصلة بين العقد، بحيث تمثل العقدة بالمدينة، و المطلوب هو تحديد المسار الأمثل للوصول من المحافظة D إلى المحافظة H.



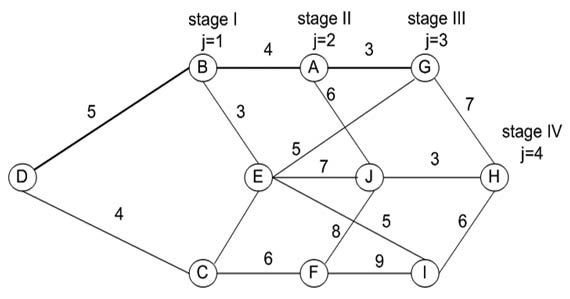
الحل:
 

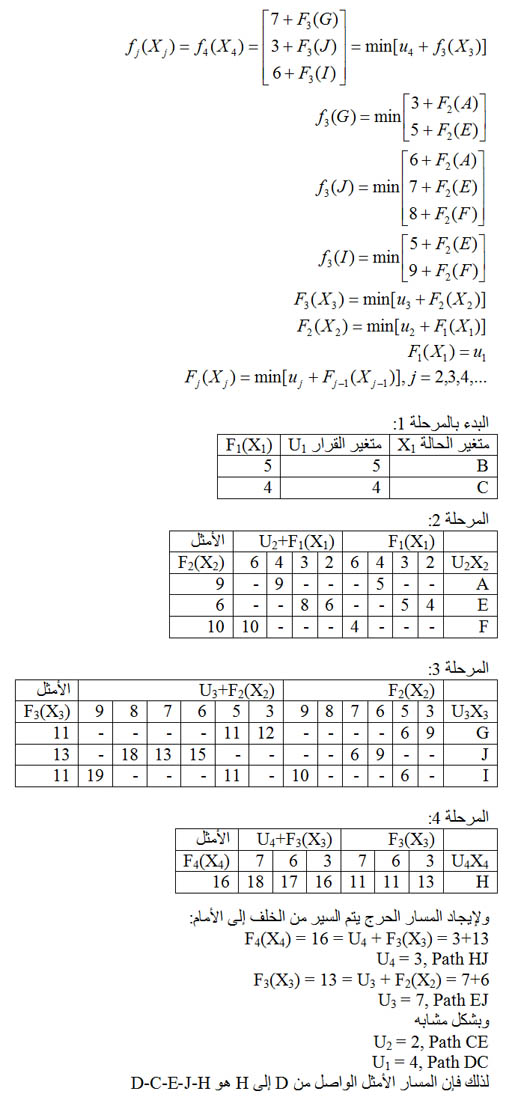
اعتذر على الاطالة... واتمنى ان تكون المعلومات ذات فائدة... وسأحاول في أقرب فرصة في تلخيص خوارزمية فلويد وشرحها ضمن مشاركات قادمة بإذن الله.

السلام عليكم

جزاك الله خيرا استاذ همام وشكرا علي الرد 😄

بصراحة طريقة ال Dynamic Programming والشرح الذي حضرتك ذكرته درسناه في الكلية في السنة الثالثة وكانت الدراسة بالفعل تتعلق ببحوث العمليات
وبالتحديد ال optimization and transportations problems

في انتظار شرح حضرتك لطريقة استخراج المسار من طريقة Floyd

بالمناسبة انا ايضا لم اسمع عن هذه الخوارزمية من قبل لكن الدكتور المشرف علي مشروع تخرجي طلب مننا ان نقوم بعمل برنامج بسيط يقوم بمقارنة
كلا من A* and Dijkstra's and Floyd ولقد قمت بالتطبيق بالفعل الا ان خوارزمية فلويد  لم استطع ان استخرج المسار من المصفوفة الناتجة النهائية

كنت قرأت ايضا عن بحث حديث حول استخدام ال HPA* او ال Hierarchal PathFinding using A*  وذلك بعمل وتطبيق ال path finding علي
 هيئة Layered AI وهذه الطريقة مشهورة علي ما اعتقد في البيئات الكبيرة وذلك بتقسيم البيئة الي high level graph وتطبيق خوارزم ايجاد مسار مناسب
ثم تطبيق الخوارزم نفسه مرة اخري او خوارزم اخر علي ال sub-graph التي فيها المكان المراد الانتقال اليه
- اسم البحث هو
Hierarchical Pathfinding and AI-Based Learning Approach in Strategy Game Design

بصراحة ان الديمو الذي اريد عمله لمشروع التخرج هو مشابه جدا للاتي

مع تبسيط المشهد قليلا وذلك بتطبيق خوارزميات طرق ايجاد المسار كأنها في بيئة ثنائية البعد فقط

فما رايك هل بيئة بهذا الحجم يناسبها خوارزم مثل الـفلويد وهو الذي يقوم بالحساب لكل نقطتين between every 2 nodes
او يمكننا فقط استخدامه عند التطبيق لاي sub-graph في حالة اننا قسمنا البيئة لعدد من ال quads

شكرا اخي همام مرة اخري
وفي انتظار سماع المزيد قريبا

السلام عليكم

لقد راجعت طريقة فلويد مرة اخري وفهمتها بحمد الله
وهذا شرح مبسط

بفرض ان لدينا ال graph الاتيه



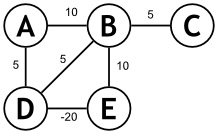
اول خطوة هي تحويل هذه ال graph الي مصفوفة تحتوي القيم التي تبين التكلفة بين كل node والاخري
بشرط ان نضع القيمة  0 في حالة لم يكن هناك edge مباشرة بين اي two nodes
فيكون لدينا المصفوفة الاتية

initial matrix:-

	A	B	C	D	E
A	0	10	oo	5	oo
B	10	0	5	5	10
C	oo	5	0	oo	oo
D	5	5	oo	0	20
E	oo	10	oo	20	0

ملاحظة : للتوضيح فقط لقد وضعت القيمة oo وتعني ما لا نهاية في حالة لم يوجد وصلة بين اي two nodes

بعد انشاء هذه المصفوفة نقوم بعمل loop وعدد ال iterations يساوي عدد ال nodes
مثال مع اول iteration للـ node A

iteration no. 1
	A	B	C	D	E
A	0	10	15	5	20
changes in C - E

هنا نضع ال node المراد العمل عليها في ال iteration الحالية علي هيئة صف وقيمه مأخوذة من ال initial matrix
نلاحظ القيمة صفر والتي تعني ان ال node هي نفسها يعني اننا ننتقل من ال node A to A وهذا بالطبع لا يكلف شيئا
المسافة بين ال node A والـ node B هي 10
بالمثل بالنسبة لباقي الـ nodes

واليكم كافة ال iterations مع المصفوفة الابتدائية ومصفوفة الحل النهائي

initial matrix:-

	A	B	C	D	E
A	0	10	oo	5	oo
B	10	0	5	5	10
C	oo	5	0	oo	oo
D	5	5	oo	0	20
E	oo	10	oo	20	0


iteration no. 1
	A	B	C	D	E
A	0	10	15	5	20
changes in C - E


iteration no. 2
	A	B	C	D	E
B	10	0	5	5	10
changes in (no changes)


iteration no. 3
	A	B	C	D	E
C	15	5	0	10	15
changes in A - D - E


iteration no. 4
	A	B	C	D	E
D	5	5	10	0	15
changes in C - E


iteration no. 5
	A	B	C	D	E
E	20	10	15	15	0
changes in A - C - D



so the final matrix is
	A	B	C	D	E
A	0	10	15	5	20
B	10	0	5	5	10
C	15	5	0	10	15
D	5	5	10	0	15
E	20	10	15	15	0

هذه الطريقة يمكننا عمل الكود اللازم لها كالاتي

This is the actual algorithm:

# dist(i,j) is "best" distance so far from vertex i to vertex j 

# Start with all single edge paths.
 For i = 1 to n do
     For j = 1 to n do
         dist(i,j) = weight(i,j) 

 For k = 1 to n do # k is the `intermediate' vertex
     For i = 1 to n do
         For j = 1 to n do
             if (dist(i,k) + dist(k,j) < dist(i,j)) then # shorter path?
                 dist(i,j) = dist(i,k) + dist(k,j)

#include 

int n; /* Then number of nodes */
int dist[16][16]; /* dist[i][j] is the length of the edge between i and j if
			it exists, or 0 if it does not */

void printDist() {
	int i, j;
	printf("    ");
	for (i = 0; i < n; ++i)
		printf("%4c", 'A' + i);
	printf("\n");
	for (i = 0; i < n; ++i) {
		printf("%4c", 'A' + i);
		for (j = 0; j < n; ++j)
			printf("%4d", dist[i][j]);
		printf("\n");
	}
	printf("\n");
}

/*
	floyd_warshall()

	after calling this function dist[i][j] will the the minimum distance
	between i and j if it exists (i.e. if there's a path between i and j)
	or 0, otherwise
*/
void floyd_warshall() {
	int i, j, k;
	for (k = 0; k < n; ++k) {
		printDist();
		for (i = 0; i < n; ++i)
			for (j = 0; j < n; ++j)
				/* If i and j are different nodes and if
					the paths between i and k and between
					k and j exist, do */
				if ((dist[i][k] * dist[k][j] != 0) && (i != j))
					/* See if you can't get a shorter path
						between i and j by interspacing
						k somewhere along the current
						path */
					if ((dist[i][k] + dist[k][j] < dist[i][j]) ||
						(dist[i][j] == 0))
						dist[i][j] = dist[i][k] + dist[k][j];
	}
	printDist();
}

int main(int argc, char *argv[]) {
	FILE *fin = fopen("dist.txt", "r");
	fscanf(fin, "%d", &n);
	int i, j;
	for (i = 0; i < n; ++i)
		for (j = 0; j < n; ++j)
			fscanf(fin, "%d", &dist[i][j]);
	fclose(fin);

	floyd_warshall();

	return 0;
}

الكود والشرح مقتبس من الرابط الاتي
http://compprog.wordpress.com/2007/11/15/all-sources-shortest-path-the-floyd-warshall-algorithm/

لكن ما كان ينقص هذه الطبخة هي كيفية استخراج المسار الذي يبين افضل او اقل الطرق تكلفة
وهو ما فهمته بحمد الله كالاتي
قمت بعمل مصفوفة تمثل ال route وقمت بعمل initialize كالاتي لها

initial route matrix:-

	A	B	C	D	E
A	1	2	3	4	5
B	1	2	3	4	5
C	1	2	3	4	5
D	1	2	3	4	5
E	1	2	3	4	5

وفي كل مرة يحدث تغيير للمسار كالاتي مثلا

iteration no. 1
	A	B	C	D	E
A	0	10	15	5	20
changes in C - E

لاحظ ان التغير هنا في حالة ال E مثلا حيث ان المسار من A to E مباشرة لا يمكن الا انه يمكننا ذلك باعتبار ان ال node الوسيطة B
تمكننا من ذلك وبالتالي نقوم بوضع القيمة التي تمثل التكلفة للانتقال من A to E through B وهي 20 في حالتنا
ونقوم بتخزين ذلك في مصفوفة ال route وذلك في كل iteration في حالة تنفيذ الخوارزم الاصلي

ومن ثم في النهاية نقوم بعرض المسار وذلك كالاتي (جزء من الكود المرفق)

void printShortestPathBetween(char i, char j)
{
	cout << "the shortest path between " << i << " and " << j << " is:\n";

	/*
	if from A to E through B
		then A = i
		and  E = j
		and  k = B
	*/

	char currentNode = i;    // 'A'
	int indexJ = (int)j-'A';
	while(currentNode != j)  
	{
		cout << currentNode << " ";
		int indexI = (int)currentNode-'A';
		currentNode = route[indexI][indexJ];
	}
	cout << j << "\n\n";
}

حيث هنا نقوم بتتبع المسار بدءا من نقطة البداية مرورا بكل النقط الوسيطة

اتمني ان تستفيدوا بهذا الشرح البسيط وفائدة هذا الخوارزم Floyd كما ذكرت سابقا انه يمكننا من ايجاد اقل الطرق تكلفة بين كل two nodes
في اي graph تم وصفها علي شكل مصفوفة

والان الي المرفقات

 
يبدو أنك سبقتني في شرح الخوارزمية 😄
 




بما أنه لديك فكرة مسبقة عن موضوع البرمجة الديناميكية، أعتقد أنه من الواضح لديك كيف أن خوارزمية فلويد شكل من أشكال البرمجة الديناميكية. وفي الحقيقة أنا مستغرب من فكرة اختيار هذه الخوارزمية أو غيرها من خوارزميات البرمجة الديناميكية للقيام باستنتاج مسارات الحركة...  ولاسيما بعد ما رأيت مقطع الفيديو 😠
لأنه وكما هو واضح من المقطع، المشكلة الأكبر التي عليك إيجاد حل لها هو التخطيط الديناميكي لمسارات الحركة بشكل فعال (Effecient Dynamic Path Planning) وفي رأيي الشخصي من الصعب جداً توظيف خوارزمية فلويد أو أي خوارزميات برمجة ديناميكية أخرى لحل مثل هذه المسألة.
إن تمكنت من القيام بهذا، أعتقد انك ستكون حققت انجاز علمي كبير في هذا المجال ☺
 

 
يبدو ان دكتورك المشرف لم يشاهد مقطع الفيديو، لأنه حتى خوارزميات A* والـ Dijkstra's غالباً لن تكون فعالة لمثل الحالة المعروضة في مقطع الفيديو... هذه الخوارزميات تناسب حالة تخطيط الحركة ضمن البيئات الساكنة. أما في الحالة المعروضة فأنت امام مشكلة تخطيط الحركة ضمن آلف العناصر المتحركة الأخرى.
اقترح عليك الاطلاع على خوارزمية D*، هذه الخوارزمية تتفوق على الـ A* في قدرتها على التعامل مع الحالات الأكثر ديناميكية وغالباً عندما يرى دكتورك المشرف مقطع الفيديو سيقترحها لك للبدأ بها.
 

 
حصلت على البحث، سأقوم بمراجعته والمشاركة بأي تفاصيل ذات أهمية حول هذا الموضوع...
 
أتمنى أن تشاركنا أي عناوين لأبحاث حول هذا الموضوع لأني حالياً أعمل في خوارزميات تخطيط الحركة وتطبيقاتها في مجال الروبوتات ضمن مجموعة بحثية في الجامعة.
 
بالتوفيق...

السلام عليكم

يبدوا ان هذا الموضوع سيكون اكثر من مجرد سؤال عن خوارزم فلويد 😄 😄


اولا: اتمني لو يقوم احد بتوضيح كيفية عمل خوارزم a star علي هذه الشبكة التي تم حلها بالفلويد


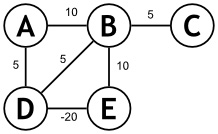
وخصوصا جزئية حساب ال  heuristic
لان الطريقة المذكورة في معظم المقالات لا تراعي حالة ال multi-cost nodes


ثانيا:- بالنسبة للبيئة الديناميكية:
بصراحة لقد قرأت في احد الافكار المعروضة في موقع ما لا اتذكره حاليا عن استخدام طريقة تشبه جدا طريقة فلويد في بيئة ديناميكية

وفكرت مبدئيا في فكرة تتلخص وتعتمد بشكل كبير علي الاعتماد علي اكثر من خوارزم معا ولكن يتم استخدام كل خوارزم في الموقف المناسب لامكاناته بحيث يمهد هذا الخوارزم لاي خوارزم اخر ليكمل العمل بعده -
الفكرة مبدئيا تتلخص في ان نقوم بعمل precomputed path planning لكل الـ way points الافتراضية لوصف الخريطة بشكل high level واذا تم حذف احد
 ال nodes ضمن اي precomputed path فنقوم باعادة جزء من عملية ال  path
planning مرة اخري وذلك باستخدام خوارزم اخر اكثر مناسبة لذلك مثل dijkstra'a حيث يتم استخدامه لايجاد كل المسارات بين هذه ال node التي تم تعديلها وبين باقي ال  nodes
يعني الفكرة تعتمد بشكل كبير علي ال hierarchical path finding


==================== 😄 😄 😄 ==================
بصراحة هناك فكرة اخري خطرت ببالي لا ادري ان كانت ممكنة وهل حقا ستقدم فارقا؟ 😒 وهي:

اولا: مبدئيا نعرف ان البيئة يتم وصفها (مثلا علي شكل grid ) في مصفوفة تمثل ذلك وبذلك يكون لدينا طبقة تمثل ال ground area لعملية البحث

كنت افكر لو يمكننا ان نقوم بحفظ البيئة كما لو كانت عدة طبقات فوق بعضها بحيث ان كل طبقة تحفظ فقط نوع واحد من بيانات البيئةوذلك في
 مصفوفة بحيث ان كل مصفوفة تحفظ فقط البيئة علي انها نوع واحد والباقي عبارة عن unwalkable nodes

>> الفكرة شبيهه جدا بموضوع ال texture blasting حيث يتم اغناء وصف
المشهد وذلك بدمج عدة طبقات اكساءات كل منها يصف اكساء للمشهد بشكل ما -
مثلا اكساء عادي للمشهد في طبقة واخر لتفاصيل اكثر في طبقة اخري واخر مثلا لوصف الاجزاء الطينية من المشهد في طبقة ثالثة وهكذا
ويتم الدمج بين الطبقات بعمل texture blending بين كل الطبقات اثناء رسم المشهد مما يتيح لنا التحكم بصورة اكبر في اثراء المشهد وذلك
باضافة ودمج طبقات اكثر تفصيلا عند الحاجة

ما اقصده بالفكرة التي خطرت علي بالي هنا بعمل نفس الفكرة ولكن للاستفادة منها في ال AI pathfinding وذلك بتجهيز عدة طبقات لوصف المشهد
وعند البحث بين اي نقطتين في البيئة نقوم باستخدام وعمل fetch من كل طبقة حسب الحاجة لمعرفة ال cost الحالية او هي اصلا قابلة للمشي
 فوقها ام لا.

طيب كيف سيسرع ذلك في الاداء - اعتقد انه مثلا اذا قمنا بحفظ طبقة تمثل المياه التي لا يمكن المشي فيها فيمكن بصورة سريعة جدا ان نعمل فحص
لمعرفة ان كان هذا المسار اصلا موجود ام لا قبل البدء في محاولة حسابه وذلك لان طبقة المياه ستبين لنا هل هناك روابط بين الجزيرة التي يراد
الانتقال منها الي المكان الهدف ام لا وذلك لانها تصف اماكن المياه بين الجزر.
(اسف ان كان الشرح غير واضح - يمكنني ان احاول التوضيح اكثر ان اردتم)


====== مثال ===== 
مثلا اذا كان لدينا بيئة مثل المذكورة هنا في الفيديو

فيمكننا ان ننشئ عدة مصفوفات بحيث كل منها تخزن فقط نوع واحد من البيانات مثلا لدينا مصفوفة يكون فيها قيم تمثل الصحراء المستوية بقيمة والباقي عبارة عن un-walkable
ولدينا مصفوفة اخري تمثل الجبال التي في الصحراء بقيمة والباقي عبارة عن un-walkable
ومصفوفة اخري لوصف اماكن البحيرات بين الجزر التي في الصحراء - واي مصفوفات اخري قد نحتاج اليها
== فمثلا لايجاد مسار حركة او طريق لكائن ما يقع في احدي الجزر ويريد ان ينتقل لجزيرة اخري وبالتالي قبل بدء البحث يمكننا سريعا ان نقوم فقط بالبحث في طبقة الجزر ونعرف هل مكان الهدف النهائي المطلوب الانتقال اليه يقع في نفس الجزيرة حيث مكان مكانه الابتدائي وهنا نبدأ بعمل البحث مباشرة بخوارزم مثل A* او ان لم يكن في نفس الجزيرة فنستخدم طبقة اخري لتساعدنا اصلا ان كان
المسار موجودا بين الجزيرة التي فيها المكان الابتدائي والجزيرة التي فيها المكان النهائي وبالتالي نستخدم ال precomputed paths المحسوبة في بداية العمل بطريقة فلويد والتي تمثل شبكة بين الجزر كلها  وهكذا نكمل البحث بالانتقال كما هو مذكور في بحث طريقة ال hierarchical
==================== 😄 😄 😄 ==================


اتمني لو كان هناك اي ملاحظات جديدة حول اي شئ قد يفيدنا في عمل المشروع بحيث يكون شبيه جدا للمذكور في الفيديو

هناك المقال الاتي http://www.ai-blog.net/archives/000152.html
بصراحة الراجل بهدل اسلوب ال way points جدا وشكله كدا بيحب ال Navigation Mesh خالص 😄

---- للاسف مع انني اعلم ان اداء طرق ايجاد البحث تعتمد جدا علي نوع البيئة المستخدمة الا ان الوقت يداهمنا من ناحية ومن ناحية اخري انا متاكد ان هناك الكثير من طرق وصف الشاهد والبيئات (خصوصا المفتوحة) قد تساعد في عملية تحسين الكفاءة - الا انني اود ان اذكر انني بغض عمل مشروع تخرج في كلية هندسة وليس مشروع بحثي بالدرجة الاولي حاليا - مما يقيدني باختيار نوع معين اعتمد عليه لتنفيذ المطلوب وكفي.
وانا هنا اتشارك معكم النقاش للاستفادة في اختيار الانسب من الخوارزميات وكذلك ال data structure المستخدم لوصف البيئة
ربما هناك العديد من العوامل الاخري الا ان هدف المشروع كما اقترحه الاخ وسام ان يكون بالتركيز علي
parallel pathfinding for numerous units
فأرجوا الا اكون خرجت عن الموضوع كثيرا بالمناقشة في هذه الامور المهمة ولكن للاسف التي قد يفتح الحوار فيها لما هو ابعد من مجرد مشروع هندسي بسيط


ايضا الاستاذ وسام ذكر في احدي المرات اسلوب ال points of visibility -
كنت اتمني لو يشاركنا احد بنبذة عنها وكيف انها قد تحسن من اداء البحث

اذا تم دمجها مع طرق البحث بالخوارزميات التقليدية؟

---- افيد علما انني قررت استخدام اطار عمل XNA كبيئة لتسهيل برمجة المشهد المذكور مع لغة السي شارب

كالعادة في انتظاركم بالملاحظات والافكار والتعليقات.
جزاكم الله خيرا

ويبدو أيضاً ان الجواب سيكون على أكثر من رد لأن مشاركتك ما شاء الله غنية بالمعلومات التي بحاجة لنقاش منفصل لكل منها على حدة.
 
 



أخي الكريم، لا أدري ماذا تقصد بحالة multi-cost nodes في الـ A*؟؟؟ عادة عند القيام بتطبيق خوارزميات البحث ضمن أي Graph او حتى Grids تكون الأوزان (Costs) على الأضلاع الواصلة بين العقد وليست على العقد نفسها وبالتالي لا وجود لـ multi-cost nodes و mono-cost nodes وإنما هناك multi-cost traverse عندما يكون لديك Directed Graph حيث يمكن أن تكون في هذه الحالة تكلفة الانتقال من عقدة معينة لاخرى لاتساوي تكلفة الانتقال بالاتجاه العكسي.
الشكل التوضيحي التالي يشرح فكرة الأوزان في حالة البحث ضمن Grids.



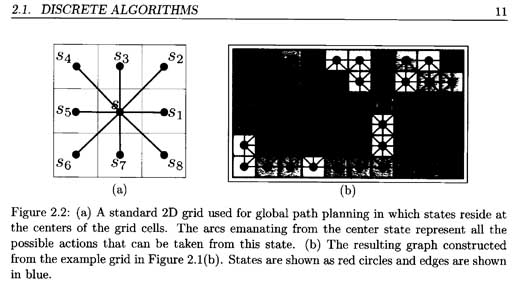
اعتذر عن عدم وضوح الصورة لأنها منقولة من أحد المراجع الأكاديمية وهي بهذا الشكل.
المرجع (1): Single Agent and Multi-agent Path Planning in Unknown and Dynamic Environments, Dave Ferguson – The Robotics Institute Carnegie Mellon University 2006

بالنسبة للمثال المعروض في خوارزمية فلويد فهو مثال كلاسيكي جداً للبحث ضمن Graph، ويمكنك تطبيق خوارزمية الـ A* بشكلها الأساسي بدون أي مشاكل. عليك فقط الانتباه لوجود أحد الأوزان ذو قيمة سالبة.

الصورة التالية توضح المبدأ الأساسي لخوارزمية الـ A* من نفس المرجع (1):



للتوضيح الخوارزمية السابقة سأحاول تقديم وشرح باختصار شديد بعض الرموز المستخدمة:
 - S ترمز للمجموعة المنتهية من الحالات الموجودة في الـ Graph.
- لأي حالتين s , s’ Є S يرمز لـ (c(s,s’ بتكلفة الضلع (edge cost) أو وزن الانتقال بين الحالاتين s و s’.
- s[start] ترمز لحالة البدء المطلوبة.
- s[end] ترمز لحالة الهدف المطلوب.
- Succ(s) ترمز للمجموعة الجزئية التي تحوي جميع الحلات المشتقة من s.
- Pred(s) ترمز للمجموعة الجزئية التي تشمل جميع الحالات السابقة للحالة s.
- المسار الناتج يتم التعبير عنه على الشكل: P={s0,s1,s2,…sn} حيث s0=s[start] و sn=s[end] و si Є Succ(si-1) لكل s.
- g(s) التكلفة المثلى المحسوبة من الحالة s[start] للحالة s المدروسة.
- h(s) التكلفة الصغرى للمسار لكل حالة s من الحالة s[goal] الى الحالة s المدروسة.

للأسف نظام الكتابة الحالي في المنتدى لم يساعدني كثيراً على التعمق في شرح الرموز والخوارزمية بشكل كافي ولكن انا جاهز لشرح اي تفصيل غير واضح.

أعتقد أنه في حال كنت معتمد على استخدام خوارزمية الـ A* من المفيد قراءة المرجع التالي:
Hart, P., Nilsson, N., and Rafael, B. (1968). A formal basis for the heuristic determination of minimum cost paths. IEEE Transactions on Systems Science and Cybernetics, 4:100-107
قد يكون المرجع قديم وتاريخي بعض الشيء ولكنه يعتبر أحد المراجع الكلاسيكية الهامة لهذه الخوارزمية.

بالنسبة لنقاش بقية المواضيع المطروحة سأخصص لها ردود لاحقة أن شاء الله.

السلام عليكم

انا في الانتظار علي احر من الجمر - وجزاك الله خيرا علي المجهود وسرعة الرد

حتي اوصل لك ما اريد فهمه بطريقة افضل
كيف سأحسب دالة ال heuristic لان حضرتك تعرف وايضا من الشرح المذكور ان هذه الدالة تقوم بحساب القيمة لمتوقعة estimated cost من النقطة
التي يتم معالجتها الان الي النقطة الهدف المراد الوصول اليها --- وانا اعلم ان هناك طرق عديدة لمثل هذه الدالة مثل طريقة  Manhattan
لمزيد من التفصيل عما اقصده يمكنك رؤية الرابط التالي http://theory.stanford.edu/~amitp/GameProgramming/Heuristics.html#S7
ولكن في حالتنا هنا في الشبكة التي تم حلها بالفلويد فان قيم ال cost بين النقط والتي تقع علي edges مختلفة من نقطة لاخري وليست متساوية
يعني اذا اردنا حساب التكلفة المتوقعة من النقطة الحالية الي الهدف فستختلف بحسب المسار الذي نأخذه
فكيف سنقوم بحساب قيمة ال H function
(ارجو ان تكون قد فهمتني)
عموما بالبحث مرة اخري وجدت الاتي:
http://khorshid.ece.ut.ac.ir/~acm/ejournal/public/pdf/from-a-star-to-lpa.pdf
ووجدت المقطع الاتي في مقالة مشهورة جدا
http://www.policyalmanac.org/games/aStarTutorial.htm
بالتحديد في جزء الذي يبدئ بـ Variable Terrain Cost: I
لكن لم يشرح كيف يتم ذلك (اتمني لو هناك مثال واضح عن افضل طريقة لتمثيل شكل ال graph داخل الكود ومثال علي حساب ال H)

شكرا لك وفي انتظار سماع المزيد قريبا

بداية اعتذر عن تأخري الشديد بالرد هذه المرة لأسباب خارجة عن ارادتي... 😨

بالنسبة لاستكمال النقاش حول تفاصيل خوارزمية الـ A*، قمت باستكمالها في مشاركة منفصلة للأسباب تنظيمية نظراً لكون النقاش تطور بشكل بعيد عن الموضوع الأساسي لهذه المشاركة "خوارزمية فلويد"...

رابط المشاركة الجديدة: "استنتاج دالة الـ heuristic لخوارزمية A*"
http://www.agdn-online.com/communities.aspx?view=posts&threadid=483