

 همام البهنسي
مشاركة 1
في 25 نوفمبر 2008 01:34 ص
همام البهنسي
مشاركة 1
في 25 نوفمبر 2008 01:34 ص
هذه المشاركة استكمال للنقاش حول خوارزمية A* المطروحة في:
http:/
عظيم، أعتقد اننا بدأنا نضع يدنا على المشكلة الحقيقية... وهو ايجاد طريقة مناسبة لاستناج التابع الرياضي لدالة الـ Heuristic!
بداية نحن نتفق أن طريقة منهاتن (Manhattan) وغيرها من الأساليب المشروحة في الروابط التي ارفقتها في مشاركتك السابقة لا تصلح لحل المسألة المعروضة في خوارمية فوليد! السبب ببساطة لأنها محدودة في معالجة حالة خاصة جداً وهي البحث ضمن شبكة ذات تكاليف نقل متساوية بين الخلايا... بالطبع هذه الحالة رغم خصوصيتها الا انها الأكثر انتشاراً وتطبيقاً في مسائل البحث عن المسار وخصوصاً في الألعاب ولكننا ما نحتاجه هنا هو استنتاج دالة رياضية عامة للتابع s)H) قادرة على حل المسألة حتى في حال اختلاف قيم الانتقال بين الحالات.
لذلك في مثل هذه الحالات العامة من الأفضل البحث ضمن المراجع الأكاديمية لكونها تهتم بشرح هذه الخوارزميات بشكل تجريدي أكثر من مراجع الألعاب التي تركز على بالجانب التطبيقي.
في الجزء التالي من المشاركة سأحاول توضيح باختصار أحد هذه الطرق العامة بالاعتماد على المرجع التالي:
Principles of Robot Motion: Theory, Algorithms, and Implementations (Intelligent Robotics and Autonomous Agents)
من نشر MIT Press وتأليف: Howie Choset, Kevin M. Lynch, Seth Hutchinson, George Kantor, Wolfram Burgard, Lydia E. Kavraki, Sebastian Thrun
يتعرض هذا المرجع لخوارزمية A* بشكل مختصر ضمن الملاحق ولكنه لا يركز عليها بسبب عدم كفائتها في حل مسائل تخطيط حركة الروبوتات، لذلك لا انصحك بمثل هذه المراجع لمشروعك لكونها تركز على أنواع مختلفة كلياً من خوارزميات تخطيط الحركة تعتمد على نظريات الاحتمالات والاستعيان العشوائي (Randomized Sampling).
لتبسيط الشرح سابدء مباشرة بالمثال المعروض في الكتاب والذي يعرض حالة عامة جداً:
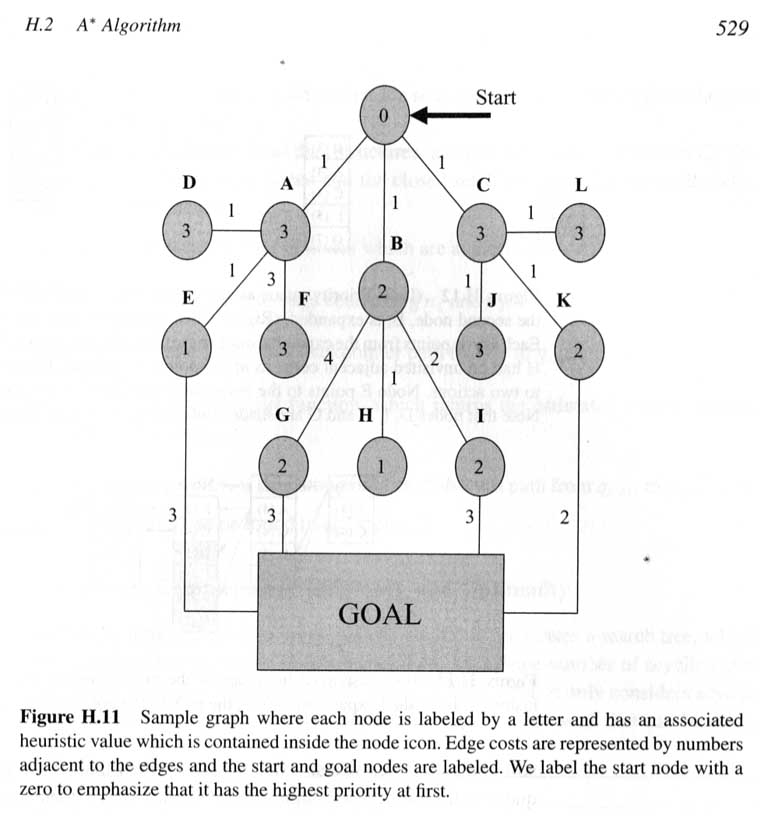
هذه المسألة رغم بساطتها إلا أنها تعالج حالة تجريدية عامة وهامة جداً في رأيي الشخصي، فلدينا كما هو واضح من الشكل:
أولاً: أوزان الانتقال المكتوبة على الاضلاع بين العقد أو الحالات غير متساوية، مثلاً تكلفة الانتقال بين الحالة B-G = 4 بينما لدينا بين B-I = 2
ثانياً: قيمة الدالة H)s) المكتوبة ضمن الدوائر تم تحديدها بشكل مسبق لكل حالة s بشكل عام دون الاعتماد على أي من الطرق المبسطة مثل منهاتن (Manhattan) وغيرها.
ثالثاً: قيمة الدالة s)H) مستقلة تماماً عن أوزان الانتقال بين الحالات. وبالتالي نحن متحررين من مشكلة عدم توازن الـ Graph المطلوب البحث ضمنه. اي من غير الضروري أن تكون قيمة الدالة s)H) المحسوبة من خلال مسار معين متساوية في حال حسابها من خلال مسارات أخرى.
بناءً على هذه الافتراضات السابقة يتم تطبيق خوارزمية الـ A* على الشبكة السابقة وباستخدام البيانات المحددة على المخطط.
لن أكرر شرح آلية تطبيق خوارزمية الـ A* مرة أخرى وإنما سأكتفي بالأشكال التوضيحية لمراحل الحل:

الى هنا الكلام جميل ولكنه للأسف كما هو واضح لم يقدم لنا طريقة صريحة لكيفية حساب قيم الـ Heuristic التي تم تحديدها على الحالات. والسبب في هذا بسيط وفي رأيي منطقي، وهو أنه قيمة الـ Heuristic هي قيمة تجريدية يمكن أن تعبر عن أي خاصية من خصائص البيئة المراد البحث ضمنها (غير المسافة طبعاً) وبالتالي عملية استنتاج التابع تترك عادة للباحث ليقوم باستنتاجه بناءً على التطبيق المطلوب.
ويؤسفني أن أقول لك أنها قد لا تكون عملية سهلة بشكل عام، فهي الى حد كبير تشابه استنتاج تابع التقييم في الخوارزمات الجينية والتي كانت لي ذكريات طويلة معه في محاولة استنتاج دالة رياضية لتخطيط موقع إنشاء مشروع مجمع سكني. 😭
لذلك بالنسبة لتابع الـ Heuristic يمكننا الاستنتاج في النهاية أنه مسألة منفصلة تتعلق بالتطبيق المراد حله... ولكن اذا افترضنا اننا نريد حل نفس الـ Graph السابق ولكن بناءً على تكاليف النقل الغير متساوية المحددة في الشكل السابق، يمكنني اقتراح خوارزمية بسيطة لحساب قيم الـ Heuristic سأسميها طريقة (دمشق) بدل من طريقة مانهاتن! 😄 لقدرتها على حل مخططات غير منتظمة مشابهة لمدينة دمشق على عكس التنظيم الشرطنجي في مناهتن!
تتلخص هذه الطريقة في الخطوات التالية:
- البدء بتحليل الـ Graph من حالة الهدف: s(goal) وتحديد قيمة التابع H(s) = 0
- الانتقال بشكل تراجعي على جميع الحالات s المرتبطة بالحالة السابقة s’.
- لكل حالة مدروسة s يتم حساب قيمة التابع H(s) من خلال أخذ القيمة الأصغر لمجموع الـ H(s’) للحالات المرتبطة بها مع إضافة تكلفة الانتقال الجديدة بين الحالة s والحالة s’.
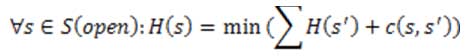
- لكل الحالات ذات النهايات المغلقة تحديد قيمة كبيرة جداً للتابع h(s):

الشكل التالي يظهر تطبيق طريقة دمشق على المخطط السابق لتحديد قيمة التابع H(s) لكل حالة ضمن المخطط.
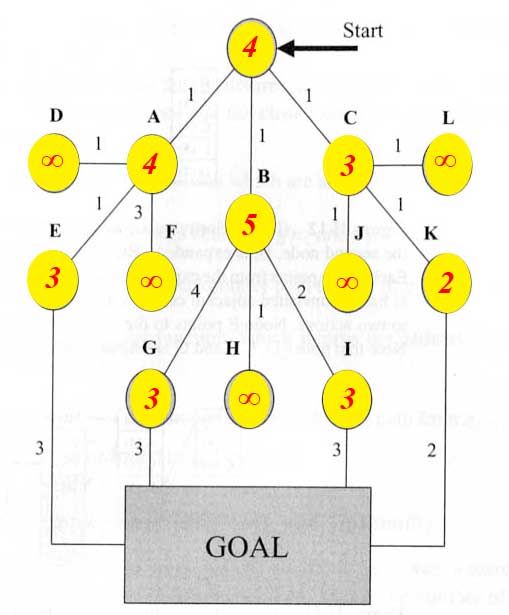
بهذا الشكل أصبح لدينا Graph يحوي جميع قيم الـ Heuristic لكل حالة بناءً على تكاليف الانتقال وبالتالي يمكننا استخدام A* ببساطة لايجاد أفضل مسار بشكل دقيق.
إذا أردنا تحليل مسألة البحث باعتماد هذا الأسلوب ستلاحظ أنها فعلياً انقسمت لمسألتين منفصلتين، الأولى هي استنتاج قيم الدالة H(s) لجميع الحالات باستخدام طريقة دمشق والتي في حقيقة الأمر ماهي إلا تطبيق مباشر لمسألة برمجة ديناميكية، المسألة الثانية هي تطبيق خوارزمية A* لاستنتاج المسار بناءً على نتائج المسألة الأولى.
لذلك وبناءً على طريقة الحل الجديدة أصبح لدينا مجموعة من الإيجابيات والسلبيات نتيجة استخدام أسلوب البرمجة الديناميكية لحل مسألة الـ Heuristics بدلاً من طريقة منهاتن التقريبية والتي يمكن تلخصيها بالنقط التالية:
1- بداية طريقة دمشق قادرة على حل المسائل غير المنتظمة على عكس طريقة منهاتن التي تفترض وجود نظام موحد في تقدير تكاليف الانتقال بين الخلايا في شبكة البحث.
2- كما هو واضح تمتاز طريقة دمشق في كونها أكثر دقة في تقدير قيمة الدالة H(s) من منهاتن التي تعتمد على حساب عدد الخلايا في الشبكة بشكل تقريبي بغض النظر عن وجود عوائق أو مسار مائل.
3- طريقة منهاتن لا تحتاج لمعالجة مسبقة للمسألة وبالتالي هي مناسبة لمسائل البحث ذات الهدف المتغير بينما طريقة دمشق تعتمد على حساب الـ Heuristics بشكل مسبق وبالتالي تناسب مسائل البحث ذات الهدف الثابت والبدء المتغير.
في النهاية أعتذر على المشاركة الطويلة وأتمنى أن أكون قد ساهمت في توضيح بعض تقنيات حساب الـ Heuristics الخاصة بخوارزمية الـ A*.
http:/
عظيم، أعتقد اننا بدأنا نضع يدنا على المشكلة الحقيقية... وهو ايجاد طريقة مناسبة لاستناج التابع الرياضي لدالة الـ Heuristic!
بداية نحن نتفق أن طريقة منهاتن (Manhattan) وغيرها من الأساليب المشروحة في الروابط التي ارفقتها في مشاركتك السابقة لا تصلح لحل المسألة المعروضة في خوارمية فوليد! السبب ببساطة لأنها محدودة في معالجة حالة خاصة جداً وهي البحث ضمن شبكة ذات تكاليف نقل متساوية بين الخلايا... بالطبع هذه الحالة رغم خصوصيتها الا انها الأكثر انتشاراً وتطبيقاً في مسائل البحث عن المسار وخصوصاً في الألعاب ولكننا ما نحتاجه هنا هو استنتاج دالة رياضية عامة للتابع s)H) قادرة على حل المسألة حتى في حال اختلاف قيم الانتقال بين الحالات.
لذلك في مثل هذه الحالات العامة من الأفضل البحث ضمن المراجع الأكاديمية لكونها تهتم بشرح هذه الخوارزميات بشكل تجريدي أكثر من مراجع الألعاب التي تركز على بالجانب التطبيقي.
في الجزء التالي من المشاركة سأحاول توضيح باختصار أحد هذه الطرق العامة بالاعتماد على المرجع التالي:
Principles of Robot Motion: Theory, Algorithms, and Implementations (Intelligent Robotics and Autonomous Agents)
من نشر MIT Press وتأليف: Howie Choset, Kevin M. Lynch, Seth Hutchinson, George Kantor, Wolfram Burgard, Lydia E. Kavraki, Sebastian Thrun
يتعرض هذا المرجع لخوارزمية A* بشكل مختصر ضمن الملاحق ولكنه لا يركز عليها بسبب عدم كفائتها في حل مسائل تخطيط حركة الروبوتات، لذلك لا انصحك بمثل هذه المراجع لمشروعك لكونها تركز على أنواع مختلفة كلياً من خوارزميات تخطيط الحركة تعتمد على نظريات الاحتمالات والاستعيان العشوائي (Randomized Sampling).
لتبسيط الشرح سابدء مباشرة بالمثال المعروض في الكتاب والذي يعرض حالة عامة جداً:

هذه المسألة رغم بساطتها إلا أنها تعالج حالة تجريدية عامة وهامة جداً في رأيي الشخصي، فلدينا كما هو واضح من الشكل:
أولاً: أوزان الانتقال المكتوبة على الاضلاع بين العقد أو الحالات غير متساوية، مثلاً تكلفة الانتقال بين الحالة B-G = 4 بينما لدينا بين B-I = 2
ثانياً: قيمة الدالة H)s) المكتوبة ضمن الدوائر تم تحديدها بشكل مسبق لكل حالة s بشكل عام دون الاعتماد على أي من الطرق المبسطة مثل منهاتن (Manhattan) وغيرها.
ثالثاً: قيمة الدالة s)H) مستقلة تماماً عن أوزان الانتقال بين الحالات. وبالتالي نحن متحررين من مشكلة عدم توازن الـ Graph المطلوب البحث ضمنه. اي من غير الضروري أن تكون قيمة الدالة s)H) المحسوبة من خلال مسار معين متساوية في حال حسابها من خلال مسارات أخرى.
بناءً على هذه الافتراضات السابقة يتم تطبيق خوارزمية الـ A* على الشبكة السابقة وباستخدام البيانات المحددة على المخطط.
لن أكرر شرح آلية تطبيق خوارزمية الـ A* مرة أخرى وإنما سأكتفي بالأشكال التوضيحية لمراحل الحل:

الى هنا الكلام جميل ولكنه للأسف كما هو واضح لم يقدم لنا طريقة صريحة لكيفية حساب قيم الـ Heuristic التي تم تحديدها على الحالات. والسبب في هذا بسيط وفي رأيي منطقي، وهو أنه قيمة الـ Heuristic هي قيمة تجريدية يمكن أن تعبر عن أي خاصية من خصائص البيئة المراد البحث ضمنها (غير المسافة طبعاً) وبالتالي عملية استنتاج التابع تترك عادة للباحث ليقوم باستنتاجه بناءً على التطبيق المطلوب.
ويؤسفني أن أقول لك أنها قد لا تكون عملية سهلة بشكل عام، فهي الى حد كبير تشابه استنتاج تابع التقييم في الخوارزمات الجينية والتي كانت لي ذكريات طويلة معه في محاولة استنتاج دالة رياضية لتخطيط موقع إنشاء مشروع مجمع سكني. 😭
لذلك بالنسبة لتابع الـ Heuristic يمكننا الاستنتاج في النهاية أنه مسألة منفصلة تتعلق بالتطبيق المراد حله... ولكن اذا افترضنا اننا نريد حل نفس الـ Graph السابق ولكن بناءً على تكاليف النقل الغير متساوية المحددة في الشكل السابق، يمكنني اقتراح خوارزمية بسيطة لحساب قيم الـ Heuristic سأسميها طريقة (دمشق) بدل من طريقة مانهاتن! 😄 لقدرتها على حل مخططات غير منتظمة مشابهة لمدينة دمشق على عكس التنظيم الشرطنجي في مناهتن!
تتلخص هذه الطريقة في الخطوات التالية:
- البدء بتحليل الـ Graph من حالة الهدف: s(goal) وتحديد قيمة التابع H(s) = 0
- الانتقال بشكل تراجعي على جميع الحالات s المرتبطة بالحالة السابقة s’.
- لكل حالة مدروسة s يتم حساب قيمة التابع H(s) من خلال أخذ القيمة الأصغر لمجموع الـ H(s’) للحالات المرتبطة بها مع إضافة تكلفة الانتقال الجديدة بين الحالة s والحالة s’.
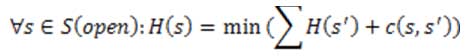
- لكل الحالات ذات النهايات المغلقة تحديد قيمة كبيرة جداً للتابع h(s):

الشكل التالي يظهر تطبيق طريقة دمشق على المخطط السابق لتحديد قيمة التابع H(s) لكل حالة ضمن المخطط.

بهذا الشكل أصبح لدينا Graph يحوي جميع قيم الـ Heuristic لكل حالة بناءً على تكاليف الانتقال وبالتالي يمكننا استخدام A* ببساطة لايجاد أفضل مسار بشكل دقيق.
إذا أردنا تحليل مسألة البحث باعتماد هذا الأسلوب ستلاحظ أنها فعلياً انقسمت لمسألتين منفصلتين، الأولى هي استنتاج قيم الدالة H(s) لجميع الحالات باستخدام طريقة دمشق والتي في حقيقة الأمر ماهي إلا تطبيق مباشر لمسألة برمجة ديناميكية، المسألة الثانية هي تطبيق خوارزمية A* لاستنتاج المسار بناءً على نتائج المسألة الأولى.
لذلك وبناءً على طريقة الحل الجديدة أصبح لدينا مجموعة من الإيجابيات والسلبيات نتيجة استخدام أسلوب البرمجة الديناميكية لحل مسألة الـ Heuristics بدلاً من طريقة منهاتن التقريبية والتي يمكن تلخصيها بالنقط التالية:
1- بداية طريقة دمشق قادرة على حل المسائل غير المنتظمة على عكس طريقة منهاتن التي تفترض وجود نظام موحد في تقدير تكاليف الانتقال بين الخلايا في شبكة البحث.
2- كما هو واضح تمتاز طريقة دمشق في كونها أكثر دقة في تقدير قيمة الدالة H(s) من منهاتن التي تعتمد على حساب عدد الخلايا في الشبكة بشكل تقريبي بغض النظر عن وجود عوائق أو مسار مائل.
3- طريقة منهاتن لا تحتاج لمعالجة مسبقة للمسألة وبالتالي هي مناسبة لمسائل البحث ذات الهدف المتغير بينما طريقة دمشق تعتمد على حساب الـ Heuristics بشكل مسبق وبالتالي تناسب مسائل البحث ذات الهدف الثابت والبدء المتغير.
في النهاية أعتذر على المشاركة الطويلة وأتمنى أن أكون قد ساهمت في توضيح بعض تقنيات حساب الـ Heuristics الخاصة بخوارزمية الـ A*.

 أحمد عزالدين
مشاركة 2
في 28 نوفمبر 2008 07:56 م
أحمد عزالدين
مشاركة 2
في 28 نوفمبر 2008 07:56 م
السلام عليكم
شكرا استاذ همام علي الشرح وجزاك الله خيرا
لكن حضرتك ذكرت المثال وهو يعتمد علي قيم H مسبقة لكل نقطة-
ولما حضرتك قمت باقتراح طريقة "دمشق" ذكرت انها مناسبة اذا كان الهدف ثابتا - ماذا ان كان الهدف متحركا في بيئة ربما تكون
ديناميكية وكذلك لعدد كبير من الوحدات والبيئة كبيرة جدا مثل RTS تماما ؟؟
مثل
حيث انني احاول ان اعمل مثل هذه البيئة لمشروع تخرجي هذا العام
جزاك الله خيرا
في انتظار ملاحظاتكم ويمكنكم ان تقوموا بالرد هناك
http:/
حيث ان الموضوع هناك ايضا يناقش البيئة وكيفية تمثيلها
والسلام عليكم
شكرا استاذ همام علي الشرح وجزاك الله خيرا
لكن حضرتك ذكرت المثال وهو يعتمد علي قيم H مسبقة لكل نقطة-
ولما حضرتك قمت باقتراح طريقة "دمشق" ذكرت انها مناسبة اذا كان الهدف ثابتا - ماذا ان كان الهدف متحركا في بيئة ربما تكون
ديناميكية وكذلك لعدد كبير من الوحدات والبيئة كبيرة جدا مثل RTS تماما ؟؟
مثل
حيث انني احاول ان اعمل مثل هذه البيئة لمشروع تخرجي هذا العام
جزاك الله خيرا
في انتظار ملاحظاتكم ويمكنكم ان تقوموا بالرد هناك
http:/
حيث ان الموضوع هناك ايضا يناقش البيئة وكيفية تمثيلها
والسلام عليكم
أحمد عزالدين
طالب دراسات عليا
جامعة كالجري
طالب دراسات عليا
جامعة كالجري